Grading On A Curve: A Look At Fingerboard Radius

A recent encounter with a re-fret opened up a whole new world with regard to the fretboard radius.

We’ve all done it.  It’s a cool guitar with a bit of a story behind it that fills a gap in your stable of shred sticks.  So you pull the trigger.  Alright.  To be fair, some of us may purchase something like that more times than we should admit.  LOL!  This one was before I started to take measuring tools with me to check out guitars.  As a result, it might be the reason why I take tools with me now.

After having this guitar about a year, I discovered the fret rocker and took it to my humble selection of guitars.  Sure, it is a neck made by a relatively known Dallas-based builder, but there were at least 5 uneven frets.  What?!?  As I’d been wanting to develop some fret-working skills, I set it aside and just didn’t play it.  Fast forward to earlier this year and when I picked up the same guitar to get more reference on those uneven frets.  I see that some frets were not seated well in the fingerboard.  Real bummer.  Also a lesson about high-dollar “prestige” builders that don’t use glue in fret slots.  HaHa!  Since I prefer to not call them out here, shoot me a message via FB for a heads-up.

Knowing that I’d totally re-fret the guitar from scratch, I removed the frets.  I put a precision straightedge to the fingerboard to make sure it was straight before moving forward.  I noticed a bit of a hump around the 3rd to 5th frets.  This means a little more work with the radius blocks than just a fast once over to prep for the new fret install.  That’s when I noticed the situation.

As this fingerboard has a compound radius, I used my gauges to confirm where each radius took hold up and down the board.  And I’ll be darned if I couldn’t find a properly matched radius across that neck.  And one radius that ran for 10 frets!  Son of a…!  There’s never an Imperial Admiral around when you really need to Force Choke someone.

 

So you may be asking, just what’s the deal with “radius” anyway?  Excellent question.

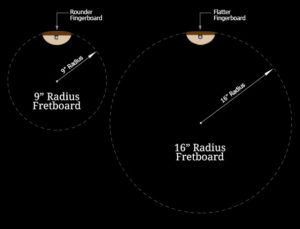
Sometimes you’ll see it referred to in degrees or inches.  For the most part, let’s just look at it in inches.  Imagine circles of different diameters.  For the sake of guitar fingerboards, some common numbers are 7.25″, 9.5″, 10″, 12″ and 16″.  Those are the radius, meaning from the center of the circle to the outer diameter.  Consequently, the smaller number has the most curve and the higher number has the least curve.

What does that have to do with me?, you ask.  Another great question.

For the most part, the smaller number with the more curved surface is considered to be a more comfortable feel for playing chords.  The bigger number with the least curved surface is considered to be better for lower action and easier bends.

Wow, you declare, it’d be great to have both!  Preach it, brother.

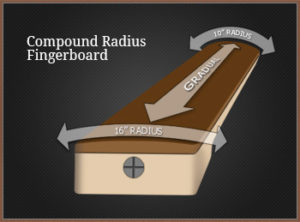
That’s where a compound radius comes in.  Sometimes called “conical” radius, which also makes sense.  Imagine a smaller radius at the nut and gradually growing, and flattening radius as you move toward the bridge.  For the most part, people consider Grover Jackson to be a pioneer in compound radius.

Aside from personal comfort, a practical consideration in the radius is the guitar’s bridge.  There are different degrees of adjustment with saddle heights on some bridges.  It might be good to consider how the different components are going to match up to help make sure you get the overall best result.  You can talk to your guitar builder or guitar tech for a more personalized approach.

Back to that hot mess of a botched fingerboard.  Having a hump in a neck is one thing.  And having an imperfect radius is another.  But having both is most lame.  Bouncing ideas around with several builders, I have a few options.  One is to totally remove the fingerboard and install a new one.  Another is to totally re-radius the fingerboard.  Yet another is to totally replace the neck.  Due to each option having a unique appeal, stay tuned to learn about which way I decide to go with this neck.

Finally, take a peek at this video of UK-based Crimson Guitars running through an approach to a compound radius: